The U.S. Pension Protection Act of 2006 (PPA) requires the calculation of the Funding Target’s Effective Interest Rate (EIR). Per Internal Revenue Code Section 430(h)(2), this is “the single rate of interest which, if used to determine the present value of the plan's accrued or earned benefits …, would result in an amount equal to the funding target of the plan for such plan year”.

If a funding run produces PPA liabilities, ProVal computes the:

• PPA funding effective interest rate based on the funding not-at-risk liability interest rate assumption if the law selection is “PPA” and based on the target liability interest rate assumption if the law selection is “Pre-PPA and PPA”.

• PPA max tax effective interest rate based on the max tax unit credit not-at-risk liability interest rate assumption if the law selection is “PPA” and, again, based on the target liability interest rate assumption if the law selection is “Pre-PPA and PPA”.

• PPA PBGC effective interest rate based on the PBGC not-at-risk liability interest rate assumption.

ProVal calculates these PPA effective interest rates using projected benefits on the “PPA EIR” basis (rather than the PPA liability basis).

In modes other than U.S. qualified and Canadian registered, funding runs (tax / funding runs in German mode) produce effective interest rates if the valuation assumption interest rate structure is constant or variable by duration from the valuation date; the effective interest rate is computed in a manner similar to that used in a PPA run. ProVal calculates the effective interest rate using projected benefits on the projected unit credit liability (PUC AL) basis if the run produces projected unit credit liabilities; otherwise, ProVal calculates the effective interest rate using projected benefits on the unit credit liability (UC AL) basis, again, if the run produces unit credit liabilities. If calculations have been performed for neither liability method, then ProVal’s effective interest rate calculation uses projected benefits on the present value of future benefits (PVB) basis.

In all modes, accounting runs produce effective discount rates if the valuation assumption interest rate structure is constant or variable by duration from the valuation date; again, the effective discount rate is computed in a manner similar to that used in a PPA run. The calculation is based on the PBO (APBO in OPEB mode) interest rate assumption and using projected benefits, for the PBO/APBO EIR, on the PBO/APBO basis, and, for the PBO/APBO normal cost EIR, on the PBO/APBO normal cost basis.  In the U.S. qualified, universal and Canadian modes, accounting runs also produce effective discount rates using projected benefits on the PBO Annuity Substitution liability and normal cost bases.  In the U.S. qualified and universal modes, no effective discount rates are calculated for either the ABO interest rate assumption or the ASC 960 interest rate assumption. In the Canadian registered mode, no effective discount rate is calculated for the ABO interest rate assumption.  

The Output variable names are “Effective Interest Rate” for funding calculations (tax/funding calculations in German mode) and “Effective Discount Rate” for accounting calculations.

If the interest rates entered are identical (for example, the same interest rates for all PPA segments or the same constant interest rates pre-decrement and post-decrement in OPEB mode), ProVal does not need to compute the effective interest rate, or effective discount rate, because it can simply set the effective interest or discount rate equal to the user-input rate.

When the interest rates entered are not identical, and thus the EIR is calculated, ProVal solves for a constant EIR, i, such that discounting a liability’s projected benefits {} using variable interest rates {} or using the constant rate, i, gets the same liability result. Ideally, ProVal would solve for i in this equation:

 

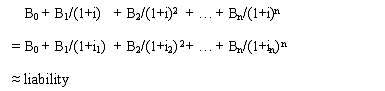
where, under a spot rate interest structure (such as for PPA liabilities), represents the interest rate used for discounting benefit payments, , made n years from the valuation date. Under a forward rate interest structure, instead, each term would have a divisor that is the product of (), i ranging from 1 to n, where represents the interest rate associated with the nth year after the valuation date. However, the value of the discounted payments produced by this equation comes close to but does not exactly match the liability (as noted by use of the “approximates” sign, instead of an equals sign). This discrepancy is due to the timing of the benefit payments, which can vary because of the payment form (annuities vs. lump sums vs. life insurance), annuity payment timing and annuity payment frequency in the pension modes, middle of year decrement timing and, in OPEB mode, timing of claims. To adjust for this, ProVal solves for the factor, k, representing the duration from the beginning of the year to the average point during the year at which projected benefit payments are assumed to be made (also referred to as the average intra-year benefit timing adjustment factor) such that the value of the discounted payments approximately equals the relevant liability (but comes closer than results from use of the equation above). Generally, the value of k ranges from 0 to 1, inclusive. Thus, under a spot rate interest structure, ProVal solves the following equation for k:

 

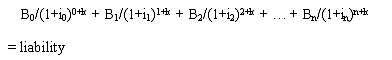
The equation to determine the EIR, i, then becomes

 

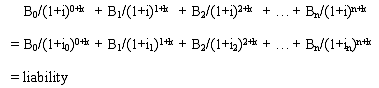
Generally, the value of k is available for display in Valuations, separately for active and inactive participants. The k factor will not be displayed in the following situations:

• In pension modes, if the interest rate structure is constant  but the interest rates entered for pre-decrement, in-deferment and/or post-commencement are not identical (or close to identical).
• In OPEB mode, if the interest rate structure is constant but the interest rates entered for pre-decrement and post-decrement are not identical and multiple runs are aggregated and the claims timing factor indicated by user input (0 for beginning of year timing, 0.5 for midyear timing and 1.0 for end of year timing) differs between any of the runs.
• Under a variable by calendar year (aka calendar year dependent) interest rate structure, because the EIR is not produced, neither the EIR nor k (the average benefit timing factor) is displayed.
• When there are no inactive participants, the average benefit timing factor for inactive participants will display as blank.When there are no active participants, the average benefit timing factor for active participants will display as blank.

In a Core Projection, the Average Benefit Timing check boxes in the Active and Inactive columns (separate Initial Inactive and Emerging Inactive columns in OPEB mode Core Projection Output) are the k factors that can be used to discount the benefit payment stream to match the corresponding liability.  They will be the same as the k factor used to determine the EIR in the initial valuation year, but may differ in the forecast years when emerging inactives are present.  The actual k-factors used in the determination of the EIR are based on 2 benefit payment streams, one combines the actives with the emerging inactives and the other is for the initial inactives. Note that for core projections run prior to ProVal version 3.10, the k-factors displayed are the ones used for the determination of the EIR, therefore, the Active column factor includes emerging inactive participants as well as continuing active participants.  The inactive factor applies to initial inactive, German terminated vested and “Vested valued through active” participants.

PPA annuities converted to lump sums on a U.S. IRC section 417(e) basis:

For plans that convert annuities to lump sums based upon IRC section 417(e) assumptions, Regulation 1.430(d)-1(f)(4)(iii)(B) describes a “substitution of annuity form” method for determining the present values of these benefits. Essentially, the lump sum present value is based on the annuity payments underlying the discounted lump sum amount. The valuation interest rates under IRC section 430(h)(2) are used for purposes of discounting the projected annuity payments from their expected payment dates to the valuation date. The applicable mortality table under IRC section 417(e)(3) that would apply to a distribution with an annuity starting date on the valuation date is substituted for the mortality table under IRC section 430(h)(3) that would otherwise be used for an annuity payment form. ProVal automatically applies this approach to Benefit Definitions with a Normal Payment Form that is an annuity Type and an Optional Payment Form that is a lump sum Type, when the valuation assumption’s Optional Payment Form conversion factors specify to use the underlying valuation interest rates. In this case, ProVal computes a separate set of expected benefit payments using the Normal Payment Form’s Benefit formula (i.e., not applying the conversion factors) and substituting the Normal Payment Form’s payment pattern (e.g., immediate life annuity), but using the lump sum’s mortality in place of IRC section 430(h) mortality.

Accounting annuities converted to lump sums:

For Benefit Definitions with a Normal Payment Form that is an annuity Type and an Optional Payment Form that is a lump sum type, if the valuation assumption’s Optional Payment Form conversion factors specify to use interest and mortality, ProVal computes PBO Annuity Substitution benefit payments. The annuity substitution benefits payments reflect the annuity stream underlying the lump sum optional form of payment (rather than reflecting the single lump sum payment). ProVal convert's the the Normal Payment Form’s Benefit formula to a lump sum using the optional form assumptions and then back to the normal form using the liability assumptions. These PBO Annuity Substitution benefit payments can be discounted back to the liability and may be used under the ASC715 and IAS19 accounting methods. See the accounting methodology topic of the Asset & Funding Policy for more details regarding available options.

1. For any payment year, all benefits are summed together before the EIR is computed. 
2. If multiple runs are summed, the projected benefits {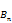} from the runs are summed before the EIR is computed. This way, you’ll get the same answer if you split your valuation into two or more runs. Note that the variable interest rates {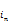} must be consistent across runs. 
3. Even when adjusting for timing (k), you won’t exactly match the liability if you rerun using the EIR as input for all valuation interest rates (e.g., for all durations from the valuation date). In empirical tests, the EIR generally was found to be accurate to four decimal places (e.g., 0.0567 or 5.67%) but sometimes was off by 0.0001 or 0.0002 (0.01% or 0.02%). 
4. When calculating an effective interest rate, ProVal currently (beginning with version 3.05) uses a tolerance of 1E-10 and will attempt to keep iterating until the estimated EIR converges to within the tolerance. This represents precision to 10 decimal places, whereas precision in earlier versions of ProVal generally was to 3 decimal places. 
5. A PPA effective interest rate is calculated (only) under a spot rate interest structure. For other types of funding liability (for example, entry age normal, projected unit credit) and for accounting liabilities, the EIR can be computed under an interest rate structure that may be either spot rates or forward rates. If the interest structure is forward rates, modifications are made to the equations above (which are based on spot rates).