Background

ProVal offers the following OPEB payment forms:

1. Life Annuity to Member

2. Life Annuity to Spouse

3. Joint Life Annuity to Spouse

4. Reversionary Annuity to Spouse

5. Life Insurance on Member's Life

6. Life Insurance on Spouse's Life

7. Lump Sum to Member, No Life Contingencies

8. Lump Sum to Member, Life Contingencies

Lifetime maximums and annual limits (caps) are relevant only to the first four payment forms listed above. Lifetime maximums and annual caps are not relevant to life insurance or lump sum payment forms because those payment forms represent one-time, rather than ongoing, payments. The remainder of this discussion pertains to lifetime maximums.

The present value for each of these payment forms (after decrement) takes the form:

Life Annuity to Member: 

Life Annuity to Spouse: 

Joint Life Annuity to Spouse: 

Reversionary Annuity to Spouse: 

Applying a lifetime maximum means substituting for in the equations above, in which is the amount of projected claims after the limit is applied. The general formula for computing is given by:

 

(1)

 

where

 

 Probability distribution function for . Probability of a contingent event occurring at time s (e.g., for a reversionary annuity, death of member) given that payment is received at time t (e.g., that member is dead at time t). s={0,1,…,t}.

 Projected claims at time t before being limited

 Projected lifetime maximum at time t

 Cumulative claims at time t, given that payment is received at time t (e.g., for a reversionary annuity, that member is dead at time t) and a contingent event occurred at time s (e.g., death of the member). s={0,1,…,t}.

 

Note that the value of is limited to zero.

 

Below we will apply equation (1) to each payment form individually and then in combination.

 

Life Annuity to Member

For a life annuity to member, it is known that the member survives in order to receive payment at time t. There are no (unknown) contingent events at time t upon which payment depends. Therefore, we can determine by:

(2)

EXAMPLE

Lifetime max: 100,000 

Discount rate: 5% 

     

t
0	10,000	100,000	0	10,000	1	1	10,000
1	10,000	100,000	10,000	10,000	0.9	0.9524	8,571
2	10,000	100,000	20,000	10,000	0.8	0.9070	7,256
3	10,000	100,000	30,000	10,000	0.7	0.8638	6,047
4	10,000	100,000	40,000	10,000	0.6	0.8227	4,936
5	10,000	100,000	50,000	10,000	0.5	0.7835	3,918
6	10,000	100,000	60,000	10,000	0.4	0.7462	2,985
7	10,000	100,000	70,000	10,000	0.3	0.7107	2,132
8	10,000	100,000	80,000	10,000	0.2	0.6768	1,354
9	10,000	100,000	90,000	10,000	0.1	0.6446	645
10	10,000	100,000	100,000	0	0	0.6139	0
						Total	47,844

 

Life Annuity to Spouse

For a life annuity to spouse, it is known that the spouse survives in order to receive payment at time t. There are no (unknown) contingent events at time t upon which payment depends, so equation (2) applies here too.

Joint Life Annuity to Spouse

For a joint life annuity to spouse, it is known that the both the member and spouse survive in order to receive payment at time t. There are no (unknown) contingent events at time t upon which payment depends, so equation (2) applies here too.

Reversionary Annuity to Spouse

For a reversionary annuity to spouse, it is known that the member dies and the spouse survives in order to receive payment. However, we do not know when the member dies. The probability that the member dies at time s given that we know the member is dead at time t is for s={0,1,…,t-1}. (Note that sum of these probabilities from s={0,1,…,t-1} should, and does, equal 1.) Applying these probabilities to the cumulative claims starting the year after the member’s death (s+1), we can determine by:

(3)

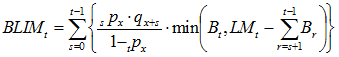
EXAMPLE

Lifetime max: 50,000 

Discount rate: 5%

 

t
0	10,000	0.1	0.1
1	10,000	0.1	0.1
2	10,000	0.1	0.1
3	10,000	0.1	0.1
4	10,000	0.1	0.1
5	10,000	1	0.1
6	10,000	1	0.1
7	10,000	1	0.1
8	10,000	1	0.1
9	10,000	1	0.1
10	10,000	1	0.1

(a). Probability of contingent events = for s={0,1,…,t-1}

	s
t	0	1	2	3	4	5	6	7	8	9
0
1	1
2	0.52632	0.47368
3	0.369	0.3321	0.29889
4	0.29078	0.2617	0.23553	0.21198
5	0.24419	0.21977	0.1978	0.17802	0.16022
6	0.1	0.09	0.081	0.0729	0.06561	0.59049
7	0.1	0.09	0.081	0.0729	0.06561	0.59049	0
8	0.1	0.09	0.081	0.0729	0.06561	0.59049	0	0
9	0.1	0.09	0.081	0.0729	0.06561	0.59049	0	0	0
10	0.1	0.09	0.081	0.0729	0.06561	0.59049	0	0	0	0

(b). Cumulative claims, given contingent events in (a) = for s={0,1,…,t-1}

	s
t	0	1	2	3	4	5	6	7	8	9	10
0
1	0
2	10,000	0
3	20,000	10,000	0
4	30,000	20,000	10,000	0
5	40,000	30,000	20,000	10,000	0
6	50,000	40,000	30,000	20,000	10,000	0
7	60,000	50,000	40,000	30,000	20,000	10,000	0
8	70,000	60,000	50,000	40,000	30,000	20,000	10,000	0
9	80,000	70,000	60,000	50,000	40,000	30,000	20,000	10,000	0
10	90,000	80,000	70,000	60,000	50,000	40,000	30,000	20,000	10,000	0

(c). Limited claims = for s={0,1,…,t-1}

	s
t	0	1	2	3	4	5	6	7	8	9	10
0
1	10,000
2	10,000	10,000
3	10,000	10,000	10,000
4	10,000	10,000	10,000	10,000
5	10,000	10,000	10,000	10,000	10,000
6	0	10,000	10,000	10,000	10,000	10,000
7	0	0	10,000	10,000	10,000	10,000	10,000
8	0	0	0	10,000	10,000	10,000	10,000	10,000
9	0	0	0	0	10,000	10,000	10,000	10,000	10,000
10	0	0	0	0	0	10,000	10,000	10,000	10,000	10,000

 

(d). Probability * Limited claims = (a) * (c) =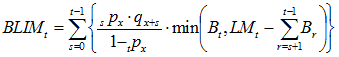

	s
t	0	1	2	3	4	5	6	7	8	9	10
0												0
1	10,000											10,000
2	5,263	4,737										10,000
3	3,690	3,321	2,989									10,000
4	2,908	2,617	2,355	2,120								10,000
5	2,442	2,198	1,978	1,780	1,602							10,000
6	0	900	810	729	656	5,905						9,000
7	0	0	810	729	656	5,905	0					8,100
8	0	0	0	729	656	5,905	0	0				7,290
9	0	0	0	0	656	5,905	0	0	0			6,561
10	0	0	0	0	0	5,905	0	0	0	0		5,905

(e). Present Value =

t
0	0	0	1	1	0.00
1	10,000	0.1	0.9	0.952381	857.14
2	10,000	0.19	0.81	0.907029	1,395.92
3	10,000	0.271	0.729	0.863838	1,706.59
4	10,000	0.3439	0.6561	0.822702	1,856.29
5	10,000	0.40951	0.59049	0.783526	1,894.66
6	9,000	1	0.531441	0.746215	3,569.13
7	8,100	1	0.478297	0.710681	2,753.33
8	7,290	1	0.430467	0.676839	2,123.99
9	6,561	1	0.38742	0.644609	1,638.51
10	5,905	1	0.348678	0.613913	1,263.99
				Total	19,059.54

 

Note: This example can be checked by comparing to the present value of a Reversionary Annuity to Spouse that continues only for 5 years after the member’s death (i.e.,).

Combinations of Payment Forms

Lifetime maximum (or annual limits) may cover Benefit Definitions with different payment forms. In this case, depends on which benefit you are valuing, as shown in equations (4), (5), (6), and (7) below. Note: is a sum of claims from all Benefit Definitions with Payment Form of:

 Life annuity to member

 Life annuity to spouse

 Joint life annuity to spouse

 Reversionary annuity to spouse

When valuing benefit i with payment form of life annuity to member, we know that the member is alive at time t. We multiply by the probability of the spouse living or dying. Notes: is paid regardless of whether the spouse lives or dies; and stop the year after the spouse’s death (s+1); is not paid because the member is known to be alive.

(4)

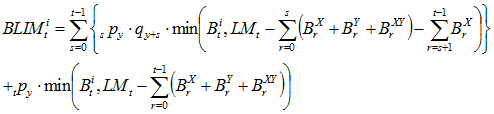
When valuing benefit i with payment form of life annuity to spouse, we know that the spouse is alive at time t. We multiply by the probability of the member living or dying. Notes: is paid regardless of whether the member lives or dies; and stop the year after the member’s death (s+1); begins the year after the member’s death (s+1).

(5)

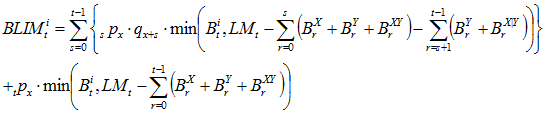
When valuing benefit i with payment form of joint life annuity to spouse, we know that both the member and spouse are alive at time t, so there are no contingent events. Note: is not paid because the member is known to be alive.

(6)

When valuing benefit i with payment form of reversionary annuity to spouse, we know that the member is dead and the spouse is alive. However, we do not know when the member died. We multiply by the probability that the member dies at time s given that we know the member is dead at time t. Notes: is paid regardless of whether the member lives or dies; and stop the year after the member’s death (s+1); begins the year after the member’s death (s+1).

(7)

 

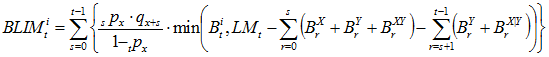
Effect of percent married and post-decrement probabilities

The equations above assume one contingent life for every primary life.  That is, if the member participates then so does the spouse (or vice versa if valuing a spouse benefit).  This will not be the case if:

• For actives, the member post-decrement probability is not equal to (the spouse post-decrement probability x percent married).

• For inactives, the percent married is not 100%.

In these cases, ProVal determines the limited claims with and without a contingent life and then weights them by their respective probabilities, that is, by the probability that the contingent life participates (or doesn’t) given that the primary life participates.

 

EXAMPLE

Family lifetime max: 100,000 

Discount rate: 5%

 

Benefit Payment Form

x Life Annuity to Member

y Life Annuity to Spouse

 

t
0	10,000	10,000	0.1	0
1	10,000	10,000	0	0
2	10,000	10,000	0	0
3	10,000	10,000	0	0
4	10,000	10,000	0	0.1
5	10,000	10,000	0	0
6	10,000	10,000	0	0
7	10,000	10,000	0	0
8	10,000	10,000	0	0
9	10,000	10,000	0	0
10	10,000	10,000	0	0

 

and represent the projected claims for benefits x and y, respectively.

and are developed below.

 

PART 1: Benefit x (x + y subject to family maximum)

(a). Probability of contingent events =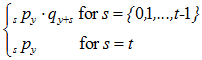

	s
t	0	1	2	3	4	5	6	7	8	9	10
0	1
1	0	1
2	0	0	1
3	0	0	0	1
4	0	0	0	0	1
5	0	0	0	0	0.1	0.9
6	0	0	0	0	0.1	0	0.9
7	0	0	0	0	0.1	0	0	0.9
8	0	0	0	0	0.1	0	0	0	0.9
9	0	0	0	0	0.1	0	0	0	0	0.9
10	0	0	0	0	0.1	0	0	0	0	0	0.9

 

(b). Cumulative claims, given contingent events in (a)

 =

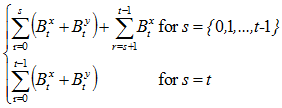
	s
t	0	1	2	3	4	5	6	7	8	9	10
0	0
1	20,000	20,000
2	30,000	40,000	40,000
3	40,000	50,000	60,000	60,000
4	50,000	60,000	70,000	80,000	80,000
5	60,000	70,000	80,000	90,000	100,000	100,000
6	70,000	80,000	90,000	100,000	110,000	120,000	120,000
7	80,000	90,000	100,000	110,000	120,000	130,000	140,000	140,000
8	90,000	100,000	110,000	120,000	130,000	140,000	150,000	160,000	160,000
9	100,000	110,000	120,000	130,000	140,000	150,000	160,000	170,000	180,000	180,000
10	110,000	120,000	130,000	140,000	150,000	160,000	170,000	180,000	190,000	200,000	200,000

(c). Limited claims =

	s
t	0	1	2	3	4	5	6	7	8	9	10
0	10,000
1	10,000	10,000
2	10,000	10,000	10,000
3	10,000	10,000	10,000	10,000
4	10,000	10,000	10,000	10,000	10,000
5	10,000	10,000	10,000	10,000	0	0
6	10,000	10,000	10,000	0	0	0	0
7	10,000	10,000	0	0	0	0	0	0
8	10,000	0	0	0	0	0	0	0	0
9	0	0	0	0	0	0	0	0	0	0
10	0	0	0	0	0	0	0	0	0	0	0

 

(d). Probability * Limited claims = (a) * (c)

	s
t	0	1	2	3	4	5	6	7	8	9	10
0	10,000											10,000
1	0	10,000										10,000
2	0	0	10,000									10,000
3	0	0	0	10,000								10,000
4	0	0	0	0	10,000							10,000
5	0	0	0	0	0	0						0
6	0	0	0	0	0	0	0					0
7	0	0	0	0	0	0	0	0				0
8	0	0	0	0	0	0	0	0	0			0
9	0	0	0	0	0	0	0	0	0	0		0
10	0	0	0	0	0	0	0	0	0	0	0	0

(e). Present Value =

t
0	10,000	1	1	10,000
1	10,000	0.9	0.952381	8,571
2	10,000	0.9	0.907029	8,163
3	10,000	0.9	0.863838	7,775
4	10,000	0.9	0.822702	7,404
5	0	0.9	0.783526	0
6	0	0.9	0.746215	0
7	0	0.9	0.710681	0
8	0	0.9	0.676839	0
9	0	0.9	0.644609	0
10	0	0.9	0.613913	0
			Total	41,914

 

PART 2: Benefit y (x + y subject to family maximum)

(a). Probability of contingent events =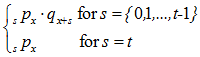

	s
t	0	1	2	3	4	5	6	7	8	9	10
0	1
1	0.1	0.9
2	0.1	0	0.9
3	0.1	0	0	0.9
4	0.1	0	0	0	0.9
5	0.1	0	0	0	0	0.9
6	0.1	0	0	0	0	0	0.9
7	0.1	0	0	0	0	0	0	0.9
8	0.1	0	0	0	0	0	0	0	0.9
9	0.1	0	0	0	0	0	0	0	0	0.9
10	0.1	0	0	0	0	0	0	0	0	0	0.9

 

(b). Cumulative claims, given contingent events in (a)

 =

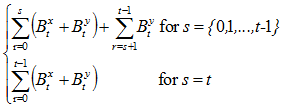
	s
t	0	1	2	3	4	5	6	7	8	9	10
0	0
1	20,000	20,000
2	30,000	40,000	40,000
3	40,000	50,000	60,000	60,000
4	50,000	60,000	70,000	80,000	80,000
5	60,000	70,000	80,000	90,000	100,000	100,000
6	70,000	80,000	90,000	100,000	110,000	120,000	120,000
7	80,000	90,000	100,000	110,000	120,000	130,000	140,000	140,000
8	90,000	100,000	110,000	120,000	130,000	140,000	150,000	160,000	160,000
9	100,000	110,000	120,000	130,000	140,000	150,000	160,000	170,000	180,000	180,000
10	110,000	120,000	130,000	140,000	150,000	160,000	170,000	180,000	190,000	200,000	200,000

(c). Limited claims =

	s
t	0	1	2	3	4	5	6	7	8	9	10
0	10,000
1	10,000	10,000
2	10,000	10,000	10,000
3	10,000	10,000	10,000	10,000
4	10,000	10,000	10,000	10,000	10,000
5	10,000	10,000	10,000	10,000	0	0
6	10,000	10,000	10,000	0	0	0	0
7	10,000	10,000	0	0	0	0	0	0
8	10,000	0	0	0	0	0	0	0	0
9	0	0	0	0	0	0	0	0	0	0
10	0	0	0	0	0	0	0	0	0	0	0

 

(d). Probability * Limited claims = (a) * (c)

	s
t	0	1	2	3	4	5	6	7	8	9	10
0	10,000											10,000
1	1,000	9,000										10,000
2	1,000	0	9,000									10,000
3	1,000	0	0	9,000								10,000
4	1,000	0	0	0	9,000							10,000
5	1,000	0	0	0	0	0						1,000
6	1,000	0	0	0	0	0	0					1,000
7	1,000	0	0	0	0	0	0	0				1,000
8	1,000	0	0	0	0	0	0	0	0			1,000
9	0	0	0	0	0	0	0	0	0	0		0
10	0	0	0	0	0	0	0	0	0	0	0	0

(e). Present Value =

t
0	10,000	1	1	10,000
1	10,000	0.952381	1	9,524
2	10,000	0.907029	1	9,070
3	10,000	0.863838	1	8,638
4	10,000	0.822702	1	8,227
5	1,000	0.783526	0.9	705
6	1,000	0.746215	0.9	672
7	1,000	0.710681	0.9	640
8	1,000	0.676839	0.9	609
9	0	0.644609	0.9	0
10	0	0.613913	0.9	0
			Total	48,085