Mortality tables with improvement scale(s) have several inputs required to calculate adjusted mortality rates:

= the base year for projecting mortality rates, e.g., 2000

= mortality base rate for a person age x in the base year y

and one of the following (either annual rates or cumulative factors): = annual rate of mortality improvement for age x in year of improvement z

= cumulative factor of mortality improvement for age x in year of improvement z

 

An adjusted mortality rate in year z is then calculated as the product of the mortality base rate and a cumulative factor of mortality improvement (described below):

= mortality rate for a life aged x in year z

In the case of an improvement scale which is of the Age by Year of Improvement type, the cumulative improvement factors F may be input directly, or annual improvement rates f may be input instead. If annual improvement rates f are entered, ProVal will calculate the cumulative factors from them as follows for the standard case z > y:

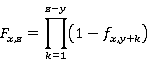
Note that the index z represents the year of the resulting adjusted mortality rate. That is, the mortality improvement from year 2000 to year 2001 is given by the year of improvement 2001 and not 2000. More information regarding this convention is available in the Society of Actuaries RPEC Response to Comments on Mortality Improvement Scale BB Exposure Draft, Section 7.8.

For the special case where z < y (e.g. for Entry Age Normal cost methods), the adjustment is instead performed as follows:

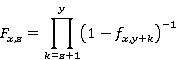
Note that if the cumulative improvement factors F are input directly, the factors in year y are expected to be 1. If they are not, the rates for each age will be normalized through division by the factors in year y:

In the simplified case that improvement scales are of the Age type (i.e. not of the Age by Year of Improvement type), they are uniform for f in all years of improvement and thus the relation above further simplifies (for any z):

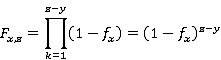
For example, consider the case with the mortality base rates and improvement scale rates here:

Age (x)	qx2000	fx,2001	fx,2002	fx,2003
65	0.012737	0.0261	0.0242	0.0230
66	0.014409	0.0275	0.0269	0.0255
67	0.016075	0.0274	0.0281	0.0278

 

With a base year of y = 2000, the adjusted mortality rates in years 2001-2003 would be calculated as follows:

Age (x)	qx	qx,2001	qx,2002	qx,2003
65	0.012737	0.012737(1-.0261) = 0.012405	0.012737(1-.0261)(1-.0242) = 0.012104	0.012737(1-.0261)(1-.0242) (1-.0230) = 0.011826
66	0.014409	0.014409(1-.0275) = 0.014013	0.014409(1-.0275)(1-.0269) = 0.013636	0.014409(1-.0275)(1-.0269) (1-.0255) = 0.013288
67	0.016075	0.016075(1-.0274) = 0.015635	0.016075(1-.0274)(1-.0281) = 0.015195	0.016075(1-.0274)(1-.0281) (1-.0278) = 0.014773

 

However, an improvement scale of the age type (without the year of improvement dimension) might instead lead to adjusted mortality rates with a simpler mortality improvement adjustment. Note that this example assumes different base rates and a different scale than the example above:

Age (x)	qx2000	fx	qx,2001	qx,2002	qx,2003
65	0.015629	0.014	0.015629(1-0.014) = 0.015410	0.015629(1-0.014)2 = 0.015194	0.015629(1-0.014)3 = 0.014982
66	0.017462	0.013	0.017462 (1-0.013) = 0.017235	0.017462 (1-0.013)2 = 0.017011	0.017462 (1-0.013)3 = 0.016790
67	0.019391	0.013	0.019391 (1-0.013) = 0.019139	0.019391 (1-0.013)2 = 0.018890	0.019391 (1-0.013)3 = 0.018645

 

The following special calculation notes apply:

• In the case of fully generational projection, the variable z (i.e. the year of improvement) represents each decrement year for the member in question. For static projection, z is instead replaced with a constant z₀ equal to the specified fixed end year, used for all decrement years for all individuals.

• Static projection leads to adjusted mortality rates that are always rounded to six decimal places.

• Generationally projected mortality rates are not rounded and will retain their full precision in subsequent calculations.