Canadian registered pension mode
ProVal calculates solvency liability and solvency incremental cost. For guidance, see the applicable provincial legislation and standards of practice of the Canadian Institute of Actuaries. The solvency incremental cost calculation in ProVal is based upon an interpretation of the CIA Educational Note “Calculation of the Incremental Cost on a Hypothetical Wind-Up or Solvency Basis”.
Solvency Liability
All inactive plan members (i.e., inactive on the valuation date), including disabled members and survivor beneficiaries, are included in the solvency liability calculation. All of their benefits are included, regardless of Payment Form. Thus, for example, a retirement Inactive Benefit with a life insurance type of Payment Form (retiree life insurance) is included.
For active plan members:
-
Immediate decrement on the valuation date is assumed (i.e., 100% of each active record retires or terminates on the valuation date). Decrement occurs at the beginning of the year, regardless of decrement timing in your Valuation Assumptions. This affects accrued benefit amounts, eligibility and payment form values.
-
If increase rates are applied to a Benefit Formula Component that is either a constant or a database field, no increases will be applied for solvency purposes since the amount as of the valuation date is used. Increase rates are applied for Benefit Formula Components that are accrual definitions (such as a cash balance account that grows with interest only to the payment date) and Benefit Formula Components that are tables.
-
Note: if "<rates by benefit>" are assumed for termination rates, an adjustment factor will be applied to benefits such that the total termination rate becomes 1. The adjustment factor for each table is based on the ratio of the original rate to the total rate.
-
Only retirement and termination benefits (Benefit Definitions) are considered in the calculation. All benefits initiated by retirement or termination are included, regardless of Payment Form. Thus, for example, a retirement Benefit Definition with a life insurance type of Payment Form (retiree life insurance) is included. All benefits initiated by death or disability are excluded.
-
At your option, immediate eligibility (e.g., vesting) for a termination benefit is presumed. If there are multiple termination benefits with different eligibilities, immediate eligibility is applied to the first termination benefit that the active member would become eligible for (in the absence of immediate vesting). If there are multiple termination benefits with the same eligibility, immediate eligibility is applied to all of those termination benefits.
-
Although use of duration-based interest rates (the transfer value rates, typically x% for 10 years, y% thereafter) is typical, you have the option to use a constant rate for participants already in receipt (as of the valuation date) and “older” participants not yet in receipt.
-
Accrued benefits (as of the valuation date) are valued, under the (pure) unit credit actuarial cost method, rather than the projected benefits at decrement that are used to compute the present value of benefits (PVB). (For further discussion of the benefits used to calculate solvency liability, see the Frequently Asked Questions article entitled “Solvency liability benefits versus PVB benefits”.) However, only those benefits (or benefit features, such as early retirement subsidies) that the member is currently eligible for (i.e., eligible for on the valuation date) are valued, unless grow-in rights apply (see below).
Election at the optimal (most valuable) age is presumed. For retirement benefits, the ages considered for election are all the future retirement-eligible ages (typically called decrement ages or retirement ages, except we won’t call them that because decrement has already occurred on the valuation date). Instead, we’ll call them election ages. For example, if your retirement rates are 100% at age 65 and retirement eligibility is coded as age 55, then ProVal considers election ages 55 through 65 (inclusive) to determine the optimal value and computes present values for each election age. Thus, in our example (and ignoring, for the time being, termination benefits), ProVal computes the present value of the benefit payable for retirement at 55, the present value of the benefit payable for retirement at 56 and so forth, up to the present value of the benefit payable for retirement at 65. ProVal selects, for the optimal age, the election age with the largest benefit present value as of the valuation date. The solvency liability basis for mortality, interest and other assumptions (as noted above) is used. For termination benefits, if considered (i.e., the member is currently eligible, or immediate eligibility is selected or grow-in rights are applied), a similar process is used. If the present value of a termination benefit for some election age exceeds all retirement election age present values, then the optimal age will be the termination benefit election age. In a common situation, a member may be entitled to a deferred normal retirement pension commencing at age 65 or a subsidized early retirement pension commencing at age 55. Generally, to determine the solvency liability, ProVal will determine the value of the pension for all ages from 55 to 65 and take the greatest of these values as of the valuation date. Besides subsidized early retirement, a participant might be eligible for a more generous payment form, such as a bridge benefit, at later ages.
ProVal calculates the optimal solvency liability value on an "aggregate" basis, i.e., the age where the value of the total solvency liability is largest is determined and ProVal then uses the value of the solvency liability at this age under all three bases: Immediate Annuity Purchase, Deferred Annuity Purchase and Transfer Value. (Thus ProVal will not, for example, take an Annuity Purchase solvency liability value at age 55 and take the Transfer Value solvency liability value at age 60.)
-
At your option, grow-in rights for selected plan members are presumed. If grow-in rights are applied, for example, for members employed in Ontario with at least 55 points (age + service) on the valuation date, then a member not yet eligible on the valuation date for particular retirement benefit(s) will be considered eligible at future election dates if the member would have become eligible at those dates had he/she remained a plan participant and the plan continued to exist, instead of terminating. Thus the value at the optimal election age is computed, assuming that a member with 55 points “grows into” eligibility. If grow-in rights are not applied, however, the value at the optimal age for this member includes the value of only the benefit(s) for which the member is currently eligible. If grow-in rights are applied and you have not selected immediate eligibility for a termination benefit, then termination benefits, as well as retirement benefits, are considered for grow-in rights.
The various solvency liability calculation options are selected in Valuation Assumptions. See Solvency Liability Transfer Value Liability, Solvency Liability Annuity Purchase Liability Solvency Liability Cost-of-Living Adjustments (COLAs) and Solvency Liability Optimal Value for more information.
The solvency liability is calculated as the greater of (a) and (b), where:
(a) = termination optimal value = if grow-in rights apply,
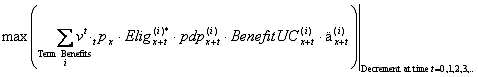
* Note: 
is adjusted for immediate eligibility, if you have selected this option.
If grow-in rights do not apply, projected eligibility 
in the equations above is replaced by eligibility on the valuation date 
.
(b) = retirement optimal value = same as (a), but for retirement benefits.
Definitions:
x = age on the valuation date.
= interest discount from election age (at t years after the valuation date) to valuation date, at post-decrement interest rate.
= probability of surviving from the valuation date to election age.
= eligibility for benefit i at election age (0 if not eligible, 1 if eligible).
= probability of receipt of benefit i at election age (typically 1), useful for valuing alternative forms, such as 80% election of lump sums and 20% election of annuities.
= projected benefit i at election age under the unit credit cost method. In general, for retirement benefits, this is the accrued benefit at age x with projected early retirement reductions at age x+t.
= payment form value (e.g., annuity value) at election age for benefit i; present value of $1 of annual benefit at election.
The optimal value calculation is similar in form to a UC liability. The differences are:
-
Because termination/retirement happens on the valuation date, the pre-decrement interest discount and survival discount factor,
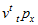, are replaced by a factor computed using post-decrement interest and mortality. Notably, the survival discount is for a single contingency, mortality. If pre-election mortality rates are zero (that is, the solvency liability mortality table is an “age by pre/post-commencement” type of table and the pre-commencement rates are all zero), then 
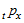is replaced by 1. -
A probability of decrement,
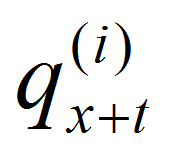, is not relevant (because we assume everyone decrements immediately). So, instead of a weighted sum of decrement age terms, 
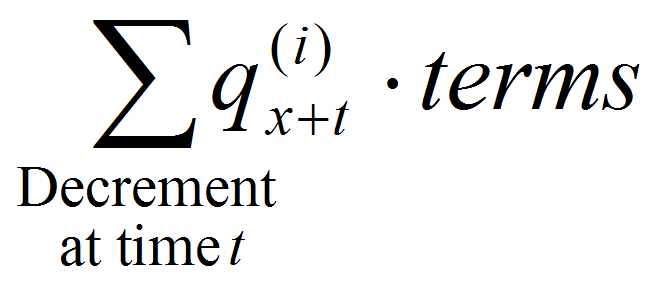, the optimal value is the maximum of terms: 
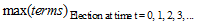. (Note that, in finding the optimal value, we look for the most valuable benefit election age, which is really a proxy for the most valuable benefit payment commencement age. Of course, if the Payment Form is payable immediately upon election, as retirement benefits often are, the election age and commencement age are identical. ProVal compares present values as of the valuation date, for all election ages, to find the age with the optimal value. -
If multiple retirement benefits exist (e.g., a regular benefit and a bridge benefit), the commuted values are summed together (across benefits) before taking the maximum value across election ages. The same is true if multiple termination benefits exist.
-
For active members, death and disability benefits are ignored.
-
Because all actives are assumed to terminate or retire on the valuation date, employee contribution “benefits” (which offset normal cost for ongoing liabilities) are ignored.
Numeric example:
The following example is based on a male participant age 45 who is entitled to a $1,000 annual termination benefit, deferred to age 65. He is projected to be eligible for early retirement at age 55, with reduction factors of 6% per year from age 65 to age 55. Grow-in rights apply. Payment Form values are based on the 1983 Group Annuity Mortality Table at 8% interest and payments are assumed made monthly.
| Termination Optimal Value: $1,000 deferred-to-65 annuity | |||||||
| Year | Age | Interest Discount | Mortality Discount | Eligibility | Accrued Benefit, b.o.y. | Payment Form Value | Present Value |
| 2004 | 45 | 1.000000 | 1.000000 | 1 | 1,000.00 | 1.627234 | 1,627.23 |
| 2005 | 46 | 0.925926 | 0.997817 | 1 | 1,000.00 | 1.761257 | 1,627.23 |
| 2006 | 47 | 0.857339 | 0.995351 | 1 | 1,000.00 | 1.906870 | 1,627.23 |
| 2007 | 48 | 0.793832 | 0.992574 | 1 | 1,000.00 | 2.065181 | 1,627.23 |
| 2008 | 49 | 0.735030 | 0.989460 | 1 | 1,000.00 | 2.237417 | 1,627.23 |
| 2009 | 50 | 0.680583 | 0.985984 | 1 | 1,000.00 | 2.424929 | 1,627.23 |
| 2010 | 51 | 0.630170 | 0.982129 | 1 | 1,000.00 | 2.629201 | 1,627.23 |
| 2011 | 52 | 0.583490 | 0.977883 | 1 | 1,000.00 | 2.851868 | 1,627.23 |
| 2012 | 53 | 0.540269 | 0.973233 | 1 | 1,000.00 | 3.094733 | 1,627.23 |
| 2013 | 54 | 0.500249 | 0.968172 | 1 | 1,000.00 | 3.359783 | 1,627.23 |
| 2014 | 55 | 0.463193 | 0.962692 | 0 | 1,000.00 | 3.649220 | 0.00 |
| 2015 | 56 | 0.428883 | 0.956790 | 0 | 1,000.00 | 3.965470 | 0.00 |
| 2016 | 57 | 0.397114 | 0.950458 | 0 | 1,000.00 | 4.311239 | 0.00 |
| 2017 | 58 | 0.367698 | 0.943673 | 0 | 1,000.00 | 4.689618 | 0.00 |
| 2018 | 59 | 0.340461 | 0.936388 | 0 | 1,000.00 | 5.104186 | 0.00 |
| 2019 | 60 | 0.315242 | 0.928538 | 0 | 1,000.00 | 5.559129 | 0.00 |
| 2020 | 61 | 0.291890 | 0.920034 | 0 | 1,000.00 | 6.059351 | 0.00 |
| 2021 | 62 | 0.270269 | 0.910775 | 0 | 1,000.00 | 6.610628 | 0.00 |
| 2022 | 63 | 0.250249 | 0.900635 | 0 | 1,000.00 | 7.219857 | 0.00 |
| 2023 | 64 | 0.231712 | 0.889476 | 0 | 1,000.00 | 7.895276 | 0.00 |
| 2024 | 65 | 0.214548 | 0.877140 | 0 | 1,000.00 | 8.646812 | 0.00 |
| Termination Optimal Value | 1,627.23 | ||||||
| Retirement Optimal Value: $1,000 immediate annuity, reduced 6% per year from 65 to 55 | |||||||
| Year | Age | Interest Discount | Mortality Discount | Eligibility | Accrued Benefit b.o.y. | Payment Form Value | Present Value |
| 2004 | 45 | 1.000000 | 1.000000 | 0 | 0.00 | 11.556700 | 0.00 |
| 2005 | 46 | 0.925926 | 0.997817 | 0 | 0.00 | 11.463929 | 0.00 |
| 2006 | 47 | 0.857339 | 0.995351 | 0 | 0.00 | 11.366930 | 0.00 |
| 2007 | 48 | 0.793832 | 0.992574 | 0 | 0.00 | 11.265661 | 0.00 |
| 2008 | 49 | 0.735030 | 0.989460 | 0 | 0.00 | 11.160039 | 0.00 |
| 2009 | 50 | 0.680583 | 0.985984 | 0 | 0.00 | 11.049938 | 0.00 |
| 2010 | 51 | 0.630170 | 0.982129 | 0 | 0.00 | 10.935136 | 0.00 |
| 2011 | 52 | 0.583490 | 0.977883 | 0 | 0.00 | 10.815361 | 0.00 |
| 2012 | 53 | 0.540269 | 0.973233 | 0 | 0.00 | 10.690269 | 0.00 |
| 2013 | 54 | 0.500249 | 0.968172 | 0 | 0.00 | 10.559449 | 0.00 |
| 2014 | 55 | 0.463193 | 0.962692 | 1 | 400.00 | 10.422457 | 1,859.00 |
| 2015 | 56 | 0.428883 | 0.956790 | 1 | 460.00 | 10.278749 | 1,940.23 |
| 2016 | 57 | 0.397114 | 0.950458 | 1 | 520.00 | 10.127775 | 1,987.77 |
| 2017 | 58 | 0.367698 | 0.943673 | 1 | 580.00 | 9.969105 | 2,006.30 |
| 2018 | 59 | 0.340461 | 0.936388 | 1 | 640.00 | 9.802503 | 2,000.05 |
| 2019 | 60 | 0.315242 | 0.928538 | 1 | 700.00 | 9.627934 | 1,972.76 |
| 2020 | 61 | 0.291890 | 0.920034 | 1 | 760.00 | 9.445534 | 1,927.81 |
| 2021 | 62 | 0.270269 | 0.910775 | 1 | 820.00 | 9.255605 | 1,868.21 |
| 2022 | 63 | 0.250249 | 0.900635 | 1 | 880.00 | 9.058673 | 1,796.67 |
| 2023 | 64 | 0.231712 | 0.889476 | 1 | 940.00 | 8.855440 | 1,715.62 |
| 2024 | 65 | 0.214548 | 0.877140 | 1 | 1,000.00 | 8.646812 | 1,627.23 |
| Retirement Optimal Value | 2,006.30 | ||||||
| Solvency Liability | |||||||
| Solvency Liability | 2,006.30 | ||||||
Solvency Incremental Cost
Because this calculation may be for a period greater than 1 year, may reflect experience assumptions that differ from the valuation assumptions and potentially reflect new entrants, incremental cost results are available only in Core Projections, not in Valuations.
The incremental cost period used in the calculation is specified under the Other Parameters topic of Projection Assumptions. Note that for a ten year forecast with a three year incremental cost period, the Core Projection has to be run for 13 projection years, because the end-of-period solvency liability used for the 10th year incremental cost would come from year 13. For this reason, incremental cost results for the last “incremental cost period” years of the Core Projection are not available.
The incremental cost calculation takes the form (1)(a) + (1)(b) – (2), where the values are defined as follows for an incremental cost being determined at time 0 and an incremental cost period of t years:
(1)(a): Experience benefit payments between time 0 and t, discounted to time 0 at the solvency liability interest rate. For this purpose, experience benefit payments corresponding to benefits with an annuity payment form are discounted using the Solvency Immediate Annuity Purchase interest rate assumption and experience benefit payments corresponding to benefits with a lump sum or life insurance payment form are discounted using the Solvency Transfer Value interest rate assumption. No experience benefit payments are discounted using the Solvency Deferred Annuity Purchase interest rate assumption. For discounting purposes, all experience benefit payments are assumed to be paid in the middle of the year. Please note that experience benefit payments for death and disability are included, even though death and disability benefits are not included in the solvency liability itself.
(1)(b): Projected solvency liability at time t, discounted to time 0 using the solvency liability interest rate assumption. In the case where more than one solvency liability interest rate is used, each component of the solvency liability at time t is discounted using the interest rate underlying the liability being discounted. As with all liabilities in a Core Projection, if a variable interest rate assumption (yield curve) is used, the liability at time t will be based on the same interest assumptions as time 0. For example, if the transfer value interest rate at time 0 is 5.0% for 10 years and 6.0% thereafter, the transfer value interest rate at time t will also be 5.0% for 10 years and 6.0% thereafter. The solvency liability at time t also reflects new entrants in accordance with 1) the Projection Assumptions and the new entrant database file, 2) Plan Amendments effective through time t that are specified in the Projection Assumptions and 3) experience cost of living adjustments (COLAs) equal to the Ongoing Liability valuation assumption COLAs.
(2): solvency liability at time 0
The solvency incremental cost is calculated as (1)(a) + (1)(b) – (2) for each individual participant. Results by individual participant are available for display in the Incremental Cost sample life report, which is displayed whenever the solvency liability sample life report is selected. The results by participant are summed into a single result, which is available as a Core Projection output item.