also used for “Sum of Digits” method
Under this asset valuation method, you specify the number of years in the averaging period of a specified historical performance index (e.g., S&P index) and the relative weight for the weighted average each year. Typically the relative weights are higher for recent values (such as in the example below), but level weights of 1 on each value can also be specified. You may code either a “classic” n-year average method or a variation known as the “sum of digits” method, discussed in a separate section at the end of this article.
Once you specify the Years in Averaging Period, a spreadsheet becomes accessible in which you enter the Performance Index values and Relative Weight to give the values associated with each relevant prior Year (one year less than the number of years in the averaging period) and with the current Year, Year 0 (year beginning on the Valuation Date (for accounting asset valuation methods, the year beginning on the Measurement Date). Year -1 is the year ending on the Valuation Date (for accounting asset valuation methods, the year ending on the Measurement Date); Year -2 (relevant for N greater than 2) is the year immediately preceding the year ending on the Valuation Date or Measurement Date, and so forth. In a forecast, ProVal will average the historical values entered (as appropriate for the future valuation date) with values it determines for future years in the averaging period.
You may apply a “growth index” to historical index values before calculating their weighted average. Check the Apply growth rate equal to valuation interest rate box to use a growth index. The growth rate generally is set equal to the funding interest rate for the actuarial value of assets and to the accounting expected return on assets for the market-related value of assets. In the U.S. qualified mode, if the applicable law selection is “PPA”, the interest rate used will be the rate selected for purposes of valuing an actuarial liability. In the event that no interest rate is selected for this purpose, the PPA funding effective interest rate will be used. Assuming that the index is increasing, use of a growth rate will produce a higher value of assets than if the index is not used.
Finally, you can specify that some proportion of the assets, considered fixed income assets, should not be smoothed (that is, simply use the market value), by checking the Value fixed income assets at market box. If this box is checked, the proportion of fixed income assets for the current year, Year 0, is specified by the Current fixed income allocation parameter value and the proportion for any future forecast valuation date is specified for a Deterministic Forecast under the Asset Smoothing Parameters topic of Deterministic Assumptions or for a Stochastic Forecast under the Asset Classes topic of the referenced Capital Market Simulation. The portion of assets that is not fixed income will reflect a value smoothed in accordance with the parameter settings you have entered for the N-year performance index method.
The calculation methodology used is as follows. Note that no rounding is currently employed in any of the steps.
Adjust historical indices by the appropriate growth factor. For example,
![]()
Calculate the weighted average index using user-supplied weights:
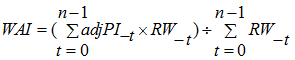
Calculate the “smoothing factor”, equal to the weighted average index divided by the current index value:
![]()
Calculate the smoothed asset value by applying the smoothing factor to that portion of the market assets subject to smoothing and then adding (to the resulting value) the full market value of any assets not subject to smoothing:
![]()
In a Deterministic Forecast, future index values are prescribed by the user under the Asset Smoothing Parameters of Deterministic Assumptions. In a Stochastic Forecast, they are determined based on the returns for equity asset classes from your Capital Market Simulation under each asset mix, applying the relative weights as described above.
As with any smoothed asset value, subject the preliminary actuarial value to the market value corridor (for example, 80% / 120%).
Example:
Below is a simple numerical example, based on:
-
Historical Performance Index of PIn-1 = 1000 with no “growth index” being applied
-
Two year equal-weighted average performance index
-
Asset mix: 40% equity class AC1 (with corresponding nominal return R1), 20% equity class AC2 (return R2) and 40% to fixed income asset classes
-
R1=18% and R2=12%, as generated by CMS
g = 40/60 * R1 + 20/60 * R2
= 16%
PIn = PIn-1 * 1.16
= 1,160
WAI = (1,000 + 1,160) / 2
= 1,080
SF = 1,080 / 1,160
= 0.931034
AVA = (0.931034 * 60% * MV) + 40% MV
= 0.958620 MV
“Sum of Digits” variation
The sum-of-digits method is similar to the N-year average method, except the asset gains/(losses) are not smoothed linearly. The sum-of-digits method applies a different weight to each year and the current year is weighted the most heavily. Set the values of the Performance Index column to be the cumulative actual returns on assets for each year included in the smoothing period. If you wish to smooth excess returns over the expected returns (instead of smoothing total returns), check the Apply growth rate equal to valuation interest rate box.
This simple example demonstrates that ProVal’s Performance Index Method, with the appropriate parameter settings, is mathematically equivalent to the sum-of-digits method. The asset information is as follows:
Current Market Value: $25,000
| Year | Gain / (Loss) | Actual Return on Assets |
| N | $2,000 | 8.6957% |
| N – 1 | $1,000 | 4.5455% |
| N – 2 | ($1,000) | -4.3478% |
| N – 3 | $2,000 | 9.5238% |
Performance index method calculation:
Based on the example above, the performance index could be parameterized as follows:
| Year | Performance Index | Relative Weight |
| - 4 | 10.00000 | 1 |
| - 3 | 10.95238 | 2 |
| - 2 | 10.47619 | 3 |
| - 1 | 10.95238 | 4 |
| 0 | 11.90476 | 5 |
(Note: Although ProVal will reflect all decimal places entered in its calculations, only two decimal places will be displayed for the performance indices and their relative weights.) In this example, a growth rate is not applied and fixed income assets are not valued at market. The performance index column was arbitrarily initialized at 10.00000 and then increased each year based on the actual return on assets. The sum of the relative weight column values is 15.
The resulting calculation is:
[(10 * 1) + (10.95238 * 2) + (10.47619 * 3) + (10.95238 * 4) + (11.90476 * 5)] / 15 = 11.11111
Adjustment Factor = 11.11111 / 11.90476 = 0.93333
AVA = 0.93333 * $25,000 = $23,333
Actual sum-of-digits calculation:
AVA = $25,000 – [(10/15) * 2,000 + (6/15) * 1,000+3/15 * (-1,000) + 1/15 * (2,000)] = $23,333.