ProVal supports the U.S. Pension Protection Act of 2006 (PPA) variable interest rate structure, under which interest rates may change every year (“spot rate curve”) or just at the 5- and 20-year marks (“segment rates”). Paraphrasing the U.S. Internal Revenue Code section 430(h)(2)(B):
-
the first segment rate is applied to benefits payable during the first 5-year period (beginning on the first day of the plan year -- or beginning on the valuation date, in this context),
-
the second segment rate is applied to benefits payable during the next 15-year period and
-
the third segment rate is applied to benefits payable thereafter.
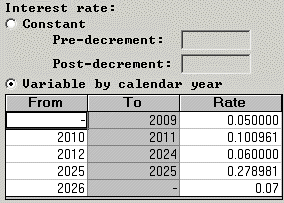
In the U.S. qualified mode, under the “PPA” and “Pre-PPA and PPA” law selections for funding valuation assumptions, options to use either the spot rate curve or segment rates are provided directly under the Interest Rates and Target Liabilities topics, respectively. For funding valuation assumptions in other modes, except for Canadian registered, and for accounting valuation assumptions in all modes, the “Variable by duration from valuation date” option with input as spot rates is provided for purposes of discounting with spot rates (or segment rates). (The “Variable by duration from valuation date” option does not apply to funding and solvency valuation assumptions in the Canadian registered mode.)
In addition, all lump sum factors and optional payment form conversion factors support use of spot interest rates as variable by duration from the valuation date or from the decrement date.
Calculating Liabilities (example using PPA segment rates)
Suppose you are valuing an annuity, paying $1,000 per year, that is deferred for 4 years and temporary for 2 years using segment rates of 5% (first 5 years), 6% (next 15 years) and 7% (thereafter).
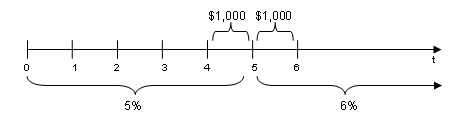
If the benefit is payable annually, at the beginning of each year, then the present value is:
![]()
If the benefit is payable monthly, at the beginning of each month, we need to adjust for monthly payments (sometimes known as the “13/24 adjustment”). The present value becomes:
![]()
Note that the interest rate curve is “discontinuous”. That is, there are discounts of both 1.05^5 and 1.06^5 at work in the equation above. Rather than a contradiction, this is merely a result of using an approximate, rather than exact, discounting of monthly benefit payments. The objective is satisfied: the first 12 payments are discounted at 5% and the other 12 payments at 6%. Graphically, the discontinuity looks like this:
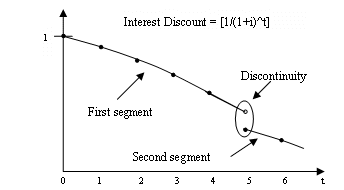
The discontinuity is a nuance based on a literal interpretation of PPA. Because of this, PPA calculations cannot be exactly duplicated by using “equivalent” rates that are “variable by calendar year”.
Checking Sample Lives: Inactive Members
Assuming segment rates of 5%, 6%, and 7%, “RP-2000 Combined Mortality” projected to 2006 using Scale AA, and an inactive life aged 67 entitled to an immediate single life annuity (paid monthly, at the beginning of each month),
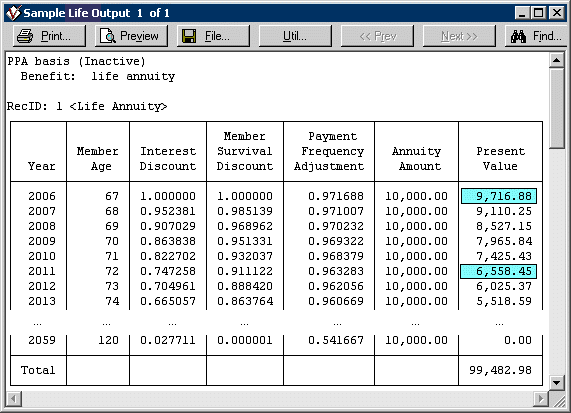
the values in the “Present Value” column above for ages 67 (first year) and 72 (sixth year) are derived as follows:
|
|
|
Checking Sample Lives: Active Members
Beginning of year decrements
The “Payment Form Values” (sometimes known as annuity factors) used to develop active liabilities are equal to the present value at decrement of future payments divided by the accrued benefit at decrement. Assuming segment rates of 5%, 6%, and 7%, “RP-2000 Combined Mortality” projected to 2006 using Scale AA, and an active life aged 67 entitled to a 10,000 immediate life annuity upon decrement at any age (paid monthly at the beginning of each month):
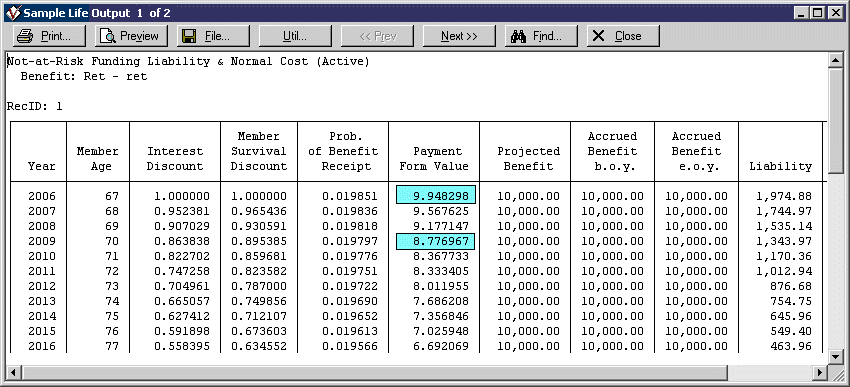
(Note: the member survival discount in this example reflects decrement rates for other contingencies besides mortality, e.g., disability.)
For decrement age 67, the payment form value is 99,482.98 / 10,000 = 9.948298. The 99,482.98 is the same present value as derived above for an inactive member. It is available for an active member from the Payment Form Value report (not shown here), on the PPA funding basis for the not-at-risk liability developed in this example.
The Payment Form Value report derives present values in this manner (example shown is for decrement age 70):

Note that the Interest Discount is normalized at decrement (i.e., made equal to 1) by multiplying by 1.05^3 (i.e., interest from the valuation date to the decrement date). While the denominator of the Interest Discount is based on 5%, 6% or 7% depending on the year the payment is expected to be paid, the numerator is a single value. The value to be used is the reciprocal of the pre-decrement Interest Discount from the above liability report (0.863838 for age 70), so that the two cancel out when determining the liability. By convention, ProVal uses the segment rate applicable to the year of decrement.
Also note that p70, p71, etc., in the payment frequency adjustment (13/24 + 11/24 v px) reflects the same member survival discount as for an inactive member, because mortality is the only contingency that applies after decrement. (Alternatively, these probabilities could have been derived from the member survival discount normalized at age 70, which we display above, instead of at age 67, as displayed in the inactive sample life report above.)
Thus we display values as of the decrement date (not the valuation date) in each row of the active sample life report (in the above example, a report for the funding not-at-risk liability).
Middle of year decrements
Under a middle of year decrement assumption, present values for actives use average benefits, average payment form values and an extra half-year interest discount.
Middle of year present value = ![]()
as compared to beginning of year present value = ![]()
where:
![]() is the pre-decrement interest discount from the decrement age to the valuation date.
is the pre-decrement interest discount from the decrement age to the valuation date.
![]() is the probability of remaining active from age x to age x+t.
is the probability of remaining active from age x to age x+t.
![]() is the probability of decrement at age x+t.
is the probability of decrement at age x+t.
![]() is the benefit amount at age x+t.
is the benefit amount at age x+t.
![]() is the present value at decrement age x+t of payments per the specified payment form (e.g. an immediate annuity). For spot rates, each payment is brought back to the valuation date at the spot rate appropriate for the payment, and then brought forward to the decrement age at the spot rate appropriate for the decrement age. For a payment due at time x+u, the interest adjustment for this payment is [(1+sx+t)x+t] / [(1+sx+u)x+u], where st is the spot rate in effect for a payment at time t.
is the present value at decrement age x+t of payments per the specified payment form (e.g. an immediate annuity). For spot rates, each payment is brought back to the valuation date at the spot rate appropriate for the payment, and then brought forward to the decrement age at the spot rate appropriate for the decrement age. For a payment due at time x+u, the interest adjustment for this payment is [(1+sx+t)x+t] / [(1+sx+u)x+u], where st is the spot rate in effect for a payment at time t.
![]() is the present value at decrement age x+t+1 of payments per the specified payment form. With a minor exception, the same interest rate assumption as for the
is the present value at decrement age x+t+1 of payments per the specified payment form. With a minor exception, the same interest rate assumption as for the ![]() (beginning of year) calculation is used. For spot rates, each payment is brought back to the valuation date at the spot rate appropriate for the payment, but with the payment assumed to be at the end of the year, and then brought forward to the decrement age at the spot rate appropriate for the decrement age.
(beginning of year) calculation is used. For spot rates, each payment is brought back to the valuation date at the spot rate appropriate for the payment, but with the payment assumed to be at the end of the year, and then brought forward to the decrement age at the spot rate appropriate for the decrement age.
When spot rates are assumed in conjunction with lump sums deferred for a period, the beginning of year spot interest rate curve is shifted forward one year for purposes of the![]() calculation. This is done in order that the present value of a lump sum payable in the middle of the year is calculated using the spot rate applicable to that year, rather than the spot rate that would be applicable if the lump sum were payable at the beginning of the following year.
calculation. This is done in order that the present value of a lump sum payable in the middle of the year is calculated using the spot rate applicable to that year, rather than the spot rate that would be applicable if the lump sum were payable at the beginning of the following year.
v 1/2 is 1/(1+i)^1/2, where i generally is the interest rate in the year of decrement. When spot interest rates are assumed, the interest discount factor at the end of the year of decrement is brought back to the valuation date and then brought forward to the beginning of the year of decrement. At decrement age x+t, v is [(1+sx+t)x+t] / [(1+sx+t+1)x+t+1], where st is the spot rate in effect for a payment at time t. There are minor exceptions to the general rule when spot rates are assumed in conjunction with certain lump sum payment forms. Please see the Technical Reference article “Decrements: beginning of year vs. middle of year” for details.
Calculating Lump Sum Factors and Optional Form Conversion Factors
When the lump sum interest basis is defined as Variable by duration from the valuation date with spot rates selected or, in the U.S. qualified mode, if Use underlying liability interest rates is selected under the “PPA” law type of funding Valuation Assumptions, you may compute the lump sum value using either the Discount to valuation Date, adjust to decrement (annuity substitution) rule or the Discount to decrement rule.
-
When the Discount to valuation Date, adjust to decrement (annuity substitution) option is selected, the lump sum factor at decrement is calculated by making an adjustment such that, when it is discounted to the valuation date, it is equivalent to valuing the annuity payments implicit in the lump sum. For U.S. qualified pension plans under the PPA law selection, this is appropriate for converting annuities to lump sums on the IRC section 417(e) interest and mortality bases as discussed in IRS Reg. 1.430(d)-1(f)(4)(iii)(B).
-
When the Discount to decrement option is selected, the unadjusted lump sum factor at decrement is used. For example, if decrement occurs four years after the valuation date, the factor is determined based on the rates as of the valuation date with the first four rates dropped. For U.S. qualified pension plans under the PPA law type, this is appropriate for converting lump sums to annuities on the IRC section 417(e) interest and mortality bases as discussed in example 14 of IRS Reg. 1.430(d)-1(f)(9) and Question 2 of the 2010 IRS Gray Book.
In Sample Lives, for a lump sum factor type of Benefit Formula Component, ProVal displays values as of the decrement date (not the valuation date) in the component sample life report, reflecting normalization at decrement of values “brought forward” from the valuation date when the “Discount to val. date, adjust to decrement (annuity sub.)” rule is selected as the spot rate method under the Lump Sum & Optional Payment Forms topic of Valuation Assumptions.
Discounting Projected Benefit Payments vs. Liabilities
On a related note, you may wonder how to discount the projected benefit payments (available in a Valuation or Valuation Set) to match a liability. A simple method of discounting is as follows:
Discount = 1 / [ (1 + i) ^ (t+0.5) ], where t=0,1,2,3,….
For example, to discount the payments described above:

Except for small variances that may arise if an estimated payment timing factor is used, the discounted benefit payments should match very closely to the liability value. See also the Frequently Asked Questions article entitled “Discounting projected benefit payments to match liabilities”.