Active decrements can be specified to occur as of the beginning or middle of the year (except German pension mode; see discussion below):

• Beginning of year calculations are determined based on the projected age, service, salary, etc., at successive decrement dates on anniversaries of the valuation date.

• Middle of year calculations are adjusted to the middle of the year, except those occurring at a 100% retirement age. In the year when the retirement rate is 100%, actives are assumed to retire immediately, at the beginning of the year.

(Note that age and service used for table lookups, however, are always determined at the beginning of the year, without regard to decrement timing. )

​

Middle of year and German decrement calculations are discussed below for:

Pension modes (other than German)
OPEB mode
German pension mode

Pension modes (other than German)

Present values for actives use average benefits with eligibility determined at middle of year, average Payment Form values and a half-year interest discount:

 

Middle of year present value =

versus

Beginning of year present value =

Where:

 is the probability of decrement at age x

 is the probability of remaining active from age x to age x+t

v is 1/(1+i), where i is the pre-decrement interest rate

 is the pre-decrement interest discount from the decrement age to the valuation date

 is the benefit amount at decrement age x

 is the benefit eligibility (either 0 for ineligible or 1 for eligible) at age x

 is the present value at decrement age x+t of payments per the specified Payment Form (e.g., an immediate annuity), reflecting any cost-of-living adjustments that may apply.

For spot rates used to value lump sums under the “annuity substitution rule”, each payment is discounted back to the valuation date at the spot rate appropriate for the payment and then brought forward to the decrement date at the spot rate appropriate for the decrement age. For a payment due at time x+u, the interest adjustment for this payment is [(1+s_x+t)^x+t] / [(1+s_x+u)^x+u], where s_t is the spot rate in effect for a payment at time t.

For spot rates used to value lump sums under the “discount to decrement” option, each payment is simply discounted to the decrement age.

 is the present value at decrement age x+t+1 of payments per the specified Payment Form. Generally, the same interest rate assumption as for the (beginning of year) calculation is used.

There is an exception to this rule when spot rates are assumed in conjunction with lump sums deferred for a specified number of years (that is, instead of deferred to a specific age):

• For spot rates under the “annuity substitution rule”, each payment is discounted back to the valuation date at the spot rate appropriate for the payment, but the payment is assumed to be at the end of the year and then the payment is brought forward to the decrement date at the spot rate appropriate for the decrement age. The beginning of year spot interest rate curve is shifted forward one year for purposes of the 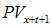calculation. This is done in order that the present value of a lump sum payable in the middle of the year is calculated using the spot rate applicable to that year, rather than the spot rate that would be applicable if the lump sum were payable at the beginning of the following year.

• For “discount to decrement” spot rates, each payment is simply discounted to the decrement age.

v^1/2 is 1/(1+i)^1/2, where i, generally, is the interest rate in the year of decrement.

When spot interest rates are assumed, the interest discount factor at the end of the year of decrement is brought back to the valuation date and then brought forward to the beginning of the year of decrement. At decrement age x+t, v is [(1+s_x+t)^x+t] / [(1+s_x+t+1)^x+t+1], where s_t is the spot rate in effect for a payment at time t.

There is an exception to this general rule when spot rates are assumed in conjunction with the following payment forms:

• Lump sums deferred for specified number of years

• Lump sums payable immediately

• Lump sums deferred to an age, if the decrement age is greater than or equal to the deferral age.

In these cases, the spot interest rate in effect at the beginning of the year is used directly.

 

Examples

Assumptions

• Segment (spot) rates = 3% (first 5 years), 5% (next 15 years), and 8% (thereafter).

• Annuity substitution rule for lump sums

• Current age (on the valuation date) = 45

• Decrement age = 45

• Decrement timing = middle of year

• Payment timing / frequency: as defined in the Payment Form Definition of each example

• Payment form values are as of the beginning of the year of decrement

 

1) Lump sum deferred to age 65, no life contingencies:

= {(1/1.08^20) + [1.03 * (1/1.08^20)]} / 2 * (1/1.03^0.5) = 0.214572

This is an approximation to 1/1.08^20 = 0.214548

 

2) Lump sum deferred 20 years from decrement, no life contingencies:

= {(1.03^0) / (1.08^20) + [(1.03^1) / (1.08^21)]} / 2 * (1/1.03^0.5) = 0.206507

This is an approximation to 1/1.08^20.5 = 0.206449

 

3) Lump sum deferred 19 years from decrement, no life contingencies:

= {(1.03^0) / (1.05^19) + [(1.03^1) / (1.05^20)]} / 2 * (1/1.03^0.5) = 0.386215

This is an approximation to 1/1.05^19.5 = 0.386197

 

NOTES:

In a Core Projection, it is possible to specify different valuation and experience assumptions with respect to when decrements occur.

If a generational mortality table is used for active mortality (i.e., the mortality table is applied prior to decrement from active status) with middle-of-year decrement timing, then the end-of-year Payment Form value that is used to get the average payment form value reflects next year’s mortality improvement.

Present value of future service and present value of future salaries can be calculated on a beginning of year, middle of year or end of year basis. This choice is independent of your selection for decrement timing.

Expected future service includes an extra half-year of service in the year of decrement.

Expected benefit payments for actives use average benefits, a half-year’s benefit payments and a half-year’s mortality. For details, see Expected benefit payments.

Projected benefit payments for actives use average benefits at decrement and average expected payments after decrement. Projected benefit payments are the terms from the middle of year present value formula at each payment age without interest. Thus, the sum of projected benefit payments exactly equals the liability at 0% interest. The formula for the projected benefit payment emanating from decrement in the middle of the year at age x+t+0.5 and paid at age s is:

 

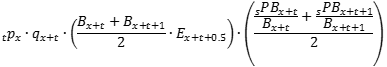
where 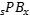is the projected benefit payment paid at age s after decrementing at the beginning of the year of age x; all other terms are as defined above for the middle of year present value. In the year of decrement (when s=x+t), the term 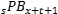is defined to be 0, resulting in a half-year payment. The averaging also results in a half-year mortality discount (if applicable) for the year of decrement that carries through to all subsequent payment ages. Note that the first year's projected benefit will generally differ slightly from the expected benefit payment because of their different methods of reflecting a half-year payment and mortality discount. For lump sums, treating each payment age separately could split the lump sum into two payments, so the portion of the average lump sum derived from decrement age x+t+1 is shifted to align with the lump sum from decrement age x+t; this only affects the timing of the payment, not the expected value of the payment.

Benefit eligibilities for actives are determined based on projected age, service and date statistics as of the middle of the year. Note that the valuation assumption for decrement timing is controlling with respect to benefit eligibilities, even though it is possible to specify contrasting valuation versus experience assumptions for this parameter in a core projection.

Employee contributions are also adjusted to the middle of the year. For details, see Employee contribution methodology.

If the valuation interest assumption is spot rates, see also Discounting with spot rates (and segment rates) and Gain and loss analysis: U.S. PPA Target Liabilities.

 

OPEB mode

Present values for actives use average payment form values and a half-year interest discount, for example:

Middle of year present value = versus

Beginning of year present value =

Where:

 is the probability of decrement at age x

 is the probability of remaining active from age x to age x+t

v is 1/(1+i), where i is the interest rate

 is a payment form value at age x

 

NOTES:

In a Core Projection, it is possible to specify different valuation and experience assumptions with respect to when decrements occur.

If a generational mortality table is used for active mortality (i.e., the mortality table is applied prior to decrement from active status) with middle-of-year decrement timing, then the end-of-year Payment Form value that is used to get the average payment form value reflects next year’s mortality improvement.

Present value of future service and present value of future salaries can be calculated on a beginning of year, middle of year or end of year basis. This choice is independent of your selection for decrement timing.

Expected benefit payments for actives use average benefits, a half-year’s benefit payments and a half-year’s mortality. For details, see Expected benefit payments.

Projected benefit payments for actives use average expected payments after decrement. Projected benefit payments are the terms from the middle of year present value formula at each payment age without interest. Thus, the sum of projected benefit payments exactly equals the liability at 0% interest. The formula for the projected benefit payment emanating from decrement in the middle of the year at age x+t+0.5 and paid at age s is:

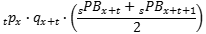
where 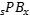  is the projected benefit payment paid at age s after decrementing at the beginning of the year of age x; all other terms are as defined above for the middle of year present value. In the year of decrement (when s=x+t), the term  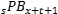 is defined to be 0, resulting in a half-year payment. The averaging also results in a half-year mortality discount (if applicable) for the year of decrement that carries through to all subsequent payment ages. Note that the first year's projected benefit will generally differ slightly from the expected benefit payment because of their different methods of reflecting a half-year payment and mortality discount. For lump sums, treating each payment age separately could split the lump sum into two payments, so the portion of the average lump sum derived from decrement age x+t+1 is shifted to align with the lump sum from decrement age x+t; this only affects the timing of the payment, not the expected value of the payment.

 

Benefit eligibilities for actives (i.e., “first” eligibility, as coded in the Eligibility section of the Benefit Definition) are determined based on projected age, service and date statistics as of the middle of the year. Note that the valuation assumption for decrement timing is controlling with respect to benefit eligibilities, even though it is possible to specify contrasting valuation versus experience assumptions for this parameter during a projection. Full eligibility for actives, however, is determined based on projected age, service and date statistics as of the beginning of the year, regardless of when decrements occur. (This is done to be consistent with the proration used for full eligibility attribution.)

See also PUC and UC Attribution.

 

German pension mode

Decrement timing is determined under Richttafeln methodology and is not a parameter the user can change. The method for determining benefit amounts and present values for actives depends on the following:

• Contingency (retirement, death, disability, etc.)

• Whether the decrement occurs directly from active service or after termination

• The method selected for Benefit determination for mid-year (death and disability) decrements in Valuation Assumptions. 

Descriptions of the calculations follow below.​

1) For retirement decrements directly from active service, and for any benefits under the Back-calculation method, no averaging takes place. Benefit service and eligibility are determined at exact retirement ages. Beginning-of-year annuity factors are used for retirement benefits, and middle-of-year annuity factors are used for death and disability benefits.

For details on middle-of-year annuity factors, see Payment form values for mid-year benefits.

 

2) For death and disability decrements directly from active service under the Valuation Date Method, present values are determined as follows:

present value A = , or

present value B = , with

option B used if the box to “apply eligibility before averaging benefits” (found under the Decrements topic of Valuation Assumptions) is checked,

 

Where:

is the probability of decrement at age x

is the probability of remaining active from age x to age x+t

v is 1/(1+i), where i is the pre-decrement interest rate

is the pre-decrement interest discount from the decrement age to the valuation date

is the benefit at decrement age x

is the benefit eligibility (either 0 for ineligible or 1 for eligible) at age x

is the mid-year present value at decrement age x based on Richttafeln methodology, which incorporates the mid-year assumption of death and disability decrements

For details, see Payment form values for mid-year benefits.

 

3) For post-termination retirement (old age) decrements, and for death and disability decrements under the Back-calculation Method, averaging takes place across the termination ages. For these retirement benefits, present values are determined as follows:

,

Where:

is the time in years from valuation age to termination age

is the benefit payable for termination at age x and retirement at age r (including vesting factors)

is the benefit eligibility (either 0 for ineligible or 1 for eligible) at retirement age r

is the present value at age x of an annuity starting at age r (beginning-of-year annuity for retirement benefits, middle-of-year for death and disability benefits)

and other symbols are as shown above in the discussion of decrements from active service.

 

4) For post-termination death or disability decrements under the Valuation Date Method, benefits are averaged to take into account the mid-year timing of both first (termination) decrement and second (death or disability) decrement. For these benefits, the benefit amount at second decrement is determined as follows:

Where:

is the time in years from valuation age to termination age

is the time in years from valuation age to second decrement age (post-termination death or disability)

is the benefit payable for the combination of termination age t₁ and second decrement age t₂ (including vesting factors)

is the benefit eligibility (either 0 for ineligible or 1 for eligible) at second decrement age x + t₂

and the present value is determined as:

, where:

is the total interest discount, applying pre-decrement interest prior to termination and post-decrement interest thereafter

is the probability that a member age x survives all causes of decrement and remains active for t years

is the probability that a member who terminated at age x survives all causes of decrement and remains terminated for t years

is the mid-year present value at second decrement age x+t2 based on Richttafeln methodology, which incorporates the mid-year assumption of death and disability decrements

 

5) For In-Service benefits, no averaging takes place, and benefit amounts are evaluated at valuation anniversaries. (Note, however, that death, disability and retirement benefits, even when included in Jubilee promises, follow the methods described in #1 and #2 above.) There is a unique payment form methodology for In-Service benefits, as described in Payment form values for mid-year benefits, in the section “In-Service Benefits in German Mode”.